Trigonometry
Trigonometry သင္ခန္းစာသည္ ၁၀ တန္းေက်ာင္းသား၊ ေက်ာင္းသူမ်ားအတြက္ ေအာင္မွတ္ေက်ာ္ျပီးဂုဏ္ထူးမွန္းသူမ်ားအတြက္ မသိမျဖစ္တဲ့ အထူးေလးက်င့္ထားရမယ့္သင္ခန္းစာပဲျဖစ္ပါတယ္။ 10 တန္းေက်ာင္းသားမွားအတြက္ Trigonometry သင္ခန္းစာကို အပိုင္းႏွစ္ပိုင္းျဖင့္ ေလ့လာစရာမ်ားျဖင့္ ျပဌာန္းေပးထားပါတယ္။ ပထမအပိုင္းမွာ စက္၀ိုင္းေလးစိတ္ေပၚက six trigonometric ration Formulae ေတြပၚမွအေျခခံတြက္ခ်က္တဲ့သင္ခန္းစာနဲ႔ ဒုတိယအပိုင္းမွTriangle ေပၚမွာအေျခခဲ့တဲ့ Law of sine and Law of Cosine ဆိုတဲ့ formulae ေတြအေပၚအေျခခံတြက္ခ်က္မွာပါ။ Trigonometric ေလးက်င့္ခန္းမ်ားသည္ က်က္မွတ္ထားေသာ formulae မ်ားကိုသာ အစားထိုးတြက္ခ်က္ထားျဖစ္ေသာေၾကာင့္ သင္ခန္းစာပါ formulae မ်ားကိုေတာ့ မရမေန ရႊတ္ဖတ္၊ ေရးက်က္၊ စူးစိုက္ၾကည့္က်က္မွတ္ေလးက်င့္ထားရပါမယ္။ ကြ်န္ေတာ့္က်က္မွတ္ပံုကေတာ့ formula တစ္ခုခ်င္းစီကို မ်က္စိ၊ ႏွတ္ျဖင့္ အာရံုစိုက္က်က္မွတ္ျပီးေသာ္ က်က္မွတ္ထားေသာ formula တိုင္းကို အေၾကာင္း ၁၀ ေလာက္ခ်ေရးက်က္မွတ္ပါသည္။ ၾကီးျမတ္တဲ့ ပညာေတြမွာ အလြယ္မရႏိုင္တာကို ေတာ့ ေက်ာင္းသားမ်ားသတိထားေစခ်င္ပါတယ္။Trigonometric Rations for Special Angles
Trigonometry ဆုိင္ရာ နယ္ပယ္ ၆ မ်ိဳးရွိပါတယ္။
- (sin) sine
- (cos) cosine
- (tan) tangent
- (cot) cotangent
- (sec) secant
- (cosec) co-secant တို႔ပဲျဖစ္ပါတယ္။
A = adjacent side ( နီးစပ္ အနား)
H = hypotenuse side ( ေထာင့္မွန္ခံ အနား)
အထက္ပါ ဇယားအရ sin ဆိုတာ O ကို တည္ျပီး H ျဖင့္စားေနသည္။ cos ဆိုသည္မွာလည္း A ကိုတည္ၿပီး H ျဖင့္စားေနသည္ဟု စသည္ျဖင့္ ၆ ခုစလံုးမွတ္သားထားပါ။ အေပၚဖက္မွ sin, cos, tan, cot, sec, cosec လို႔ အစဥ္လိုက္မွတ္သားထားပါ၊ ပိုင္းေ၀မ်ားကိုလည္း O A O A H H ႏွင့္ ပိုင္းေျခကို ေနာက္က cosec မွ sin အထိ O A O A H H ျဖင့္ေျပာင္းျပန္စီလိုက္ေသာ က်က္စရာမလို မွတ္စရာသာလိုသည္။
အထက္ပါ ႀတိဂံႏွစ္ခု နဲ႔ ဇယားကို မ်က္စိနဲ႔ က်က္မွတ္ထားရင္ six trigonometric တန္ဖိုးကို ခ်ေရးႏိုင္ပါလိမ္မယ္။ ပထမ ႀတိဂံမွ 30 degree ၏ opposite side သည္ 1 ျဖစ္ၿပီး၊ ၏ adjacent side သည္ sq root 3 ျဖစ္ျပီး 90 ဒီဂရီအတြက္ ေထာင့္မွန္ခံအနားသည္ 2 ျဖစ္သည္။ 60 degree အတြက္ မ်က္ႏွာခ်င္းဆိုင္အနား သည္ sq root 3 ျဖစ္ျပီး နီးစပ္အနားသည္ 1 ျဖစ္သည္။ sin 45 degree အတြက္ ဒုတိယ ႀတိဂံကိုၾကည့္ပါ။
စသည့္ျဖင့္ အထက္ပါရွင့္ခ်က္မ်ားကို နားလည္ေသာ 30, 45, 60 ေထာင့္မ်ားအတြက္ six trigonometric ratio မ်ားကို အလြတ္ခ်ေရးႏိုင္လိမ္မည္။ သို႔ေသာ တြက္ခ်က္ရာတြင္ အလြတ္အာဂုဏ္ေဆာင္ႏိုင္သူသည္ ပိုသာသည္။ အထက္ပါ နည္းအတိုင္းတြယ္ယူေသာ္ ေအာက္ပါဇယားအတိုင္း ရေအာင္ေလ့က်င့္ယူၿပီးက်က္မွတ္ထားက်ပါ။ က်က္ထားတာေရာမယ္ထင္ရင္ေတာ့ အထက္ပါ ႀတိဂံႏ်ွစ္ခုႏွင့္ O A O A H H ကို မွတ္မိလွ်င္လည္း အလြယ္ရွာႏိုင္ပါမည္။
- sin ေျပာင္းျပန္ cosec
- cos ေျပာင္းျပန္ sec
- tan ေျပာင္းျပန္ cot
- tan လိုခ်င္ sin ကိုတည္ cos ျဖင့္စား
- cot လိုခ်င္ cos ကိုတည္ sin ျဖင့္စား စသည္ျဖင့္က်က္မွတ္ထားပါ။
ပထမ အပိုင္းထဲတြင္ sin, cos, tan, cot, sec, cosec စသည့္ ၆ ခုလံုးသည္ positive signs မ်ားပိုင္္ဆိုင္ၾကျပီး ဒုတိယ Quadrant တြင္ sin ႏွင့္ sin ၏ေျပာင္းျပန္ျဖစ္ေသာ cosec စသည့္ ႏွစ္ခု တို႔သာ positive signs မ်ားပိုင္ဆိုင္ၾကၿပီး က်န္ေသာ cos, tan, cot, sec ေလးခုသည္ negative signs မ်ားပိုင္ဆိုင္ၾကသည္။ အထက္ပါပုံ၏ Quadrant မ်ားကိုလည္း လြယ္ကူသေဘာေပါက္မည္ထင္ပါသည္။
ေလးက်င့္ခန္းမ်ားတြက္ခ်က္ရန္ အထက္ပါအေဘာတရားမ်ားအျပင္ formula ေလးမ်ဳးိကိုလည္းက်က္မွတ္ထားရမည္။
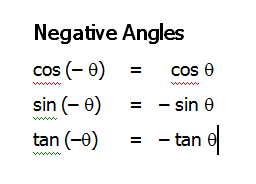
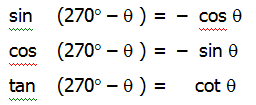
0 comments:
Post a Comment